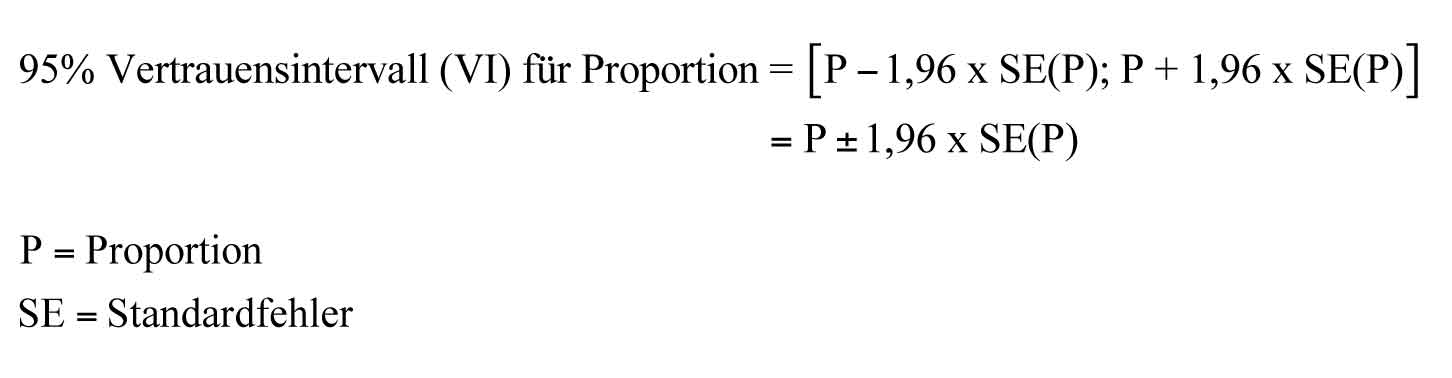Biostatistik
Marcel Zwahlen
In einem Fachartikel steht, dass bei einer bestimmten Therapieform von 100 Behandelten nur halb so viele versterben wie bei einer anderen Form der Therapie. Ist dieser Unterschied statistisch gut abgesichert (statistisch signifikant)? Oder ist es möglich, dass er nur auf Zufall beruht? Es könnte z.B. sein, dass in der ersten Gruppe eine Person verstarb, in der zweiten jedoch zwei. In der ersten Gruppe starben damit tatsächlich nur halb so viele Menschen wie in der zweiten Gruppe. Wie stark unterscheidet sich der Therapieerfolg bei diesen beiden Behandlungsformen nun wirklich? Die Statistik versucht, über numerische Informationen Antworten auf solche Fragen zu erhalten. Sie befasst sich mit dem Sammeln, Zusammenfassen, Darstellen und Interpretieren von Daten. Biostatistik ist der Zweig der Statistik, der diese Aufgaben in der Biomedizin und in Public Health übernommen hat.
Dieser Abschnitt des Lehrbuchs beschäftigt sich mit den Grundprinzipien zur Zähmung der Variabilität, d.h. die Leser erfahren hier, wie man trotz vorhandener statistischer Unsicherheit möglichst wahrheitsgemäße Schlussfolgerungen über Populationen und Patientengruppen ziehen kann. Statistik kommt dabei nicht ganz ohne mathematische Formeln aus. Sie wird daher von Vielen oftmals als schwierig oder unangenehm angesehen. Das Kapitel beschränkt deshalb den mathematischen Formalismus auf das Nötigste.
Alte Schweizerische Lernziele: CPH 13 – CPH 16
Profiles für das gesamte Kapitel 2:
GO 1.12, GO 1.15, GO 1.16, GO 1.17, GO 1.20, GO 1.24, GO 2.8, GO 4.1, GO 4.7, GO 6.5, EP 4.3
Auf dieser Seite finden Sie die in diesem Kapitel verwendeten Literaturquellen, Hinweise zu empfohlener Vertiefungsliteratur, ergänzende Abbildungen, Formeln, Tabellen und Boxen sowie weiterführende Internetquellen zum Thema.
Literaturquellen
- Kirkwood B, Sterne J. Essentials of medical statistics. 2nd Edition, Oxford: Blackwell Publishing, 2003
- Müller M. Statistik für die Pflege. Bern: Hogrefe Verlag, 2. Aufl. 2019.
- Schumacher M. Methodik klinischer Studien: Methodische Grundlagen der Planung, Durchführung und Auswertung (Statistik und ihre Anwendung) (German Edition) Berlin: Springer Verlag, 3. Aufl. 2008
Empfohlene Vertiefungsliteratur
Lehrbücher
- Benesch M, Raab-Steiner E. Klinische Studien lesen und verstehen. Stuttgart: UTB GmbH, 2. Aufl. 2018
- Kirkwood B, Sterne J. Essentials of medical statistics. 2nd Edition, Oxford: Blackwell Publishing, 2003
- Müller M. Statistik in der Pflege. Bern: Hogrefe Verlag, 2. Aufl. 2019
- Rumsey DJ. Statistik für Dummies. Weinheim: Wiley-VCH, 4. Aufl. 2015
- Schumacher M. Methodik klinischer Studien: Methodische Grundlagen der Planung, Durchführung und Auswertung (Statistik und ihre Anwendung) (German Edition) Berlin: Springer Verlag, 3. Aufl. 2008
- Weiß, C. Basiswissen Medizinische Statistik. Berlin: Springer Verlag, 7. Aufl. 2019
Zusätzliche Literatur
- Quatember A. Statistischer Unsinn. Springer Spektrum, 2015
- The American Statistician, 2019: 73
- Sterne JAC, Davey Smith G. Sifting evidence—what’s wrong with significance tests? BMJ 2001; 322: 226-231
Zusätzliche Abbildungen:
(1) Ergänzende Abbildung zu Kap. 2.3.3 Transparentes Zusammenfassen der erhobenen Daten
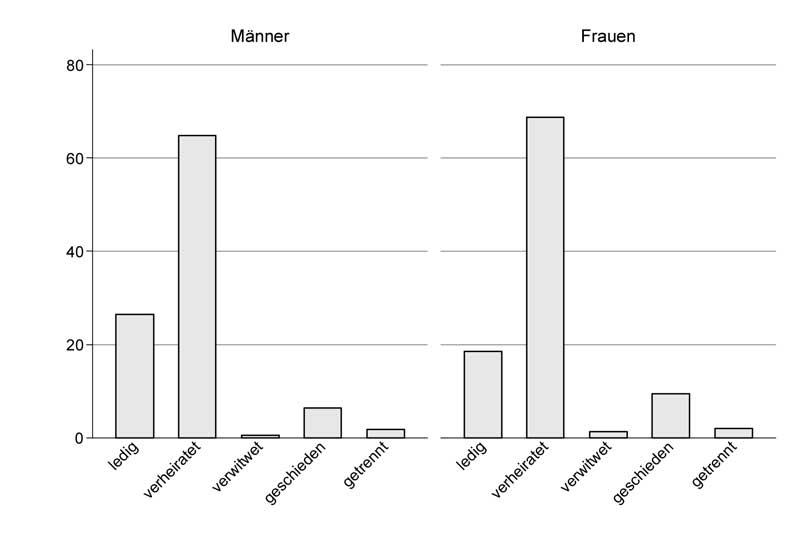
Web-Abb. 2.3.1 Häufigkeitsgrafik, die den Zivilstand (Personenstand) der 30- bis 49-jährigen Männer und Frauen in der Schweiz wiedergibt (Schweizerische Gesundheitsbefragung 2007)
(2) Ergänzende Abbildungen zu Kap. 2.3.4 Variabilität des Mittelwertes bei wiederholten Zufalls-Stichproben
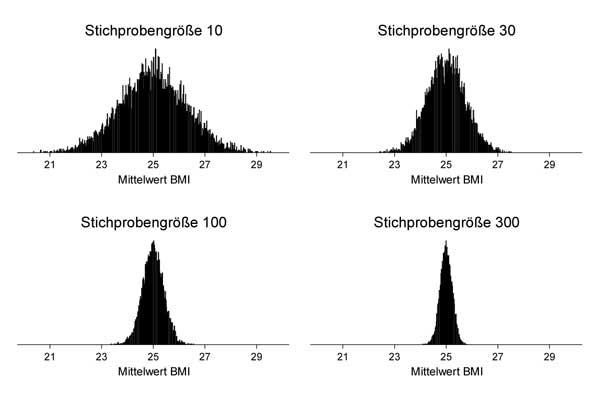
Web-Abb. 2.3.2 Stichprobenvariabilität in Abhängigkeit von der Stichprobengröße für den Mittelwert des Body Mass Index (BMI in kg/m2) bei einem wahrem Mittelwert von 25 kg/m2 und einer Standardabweichung von 4 kg/m2. Resultate von Computersimulationen mit jeweils 10.000 Stichproben
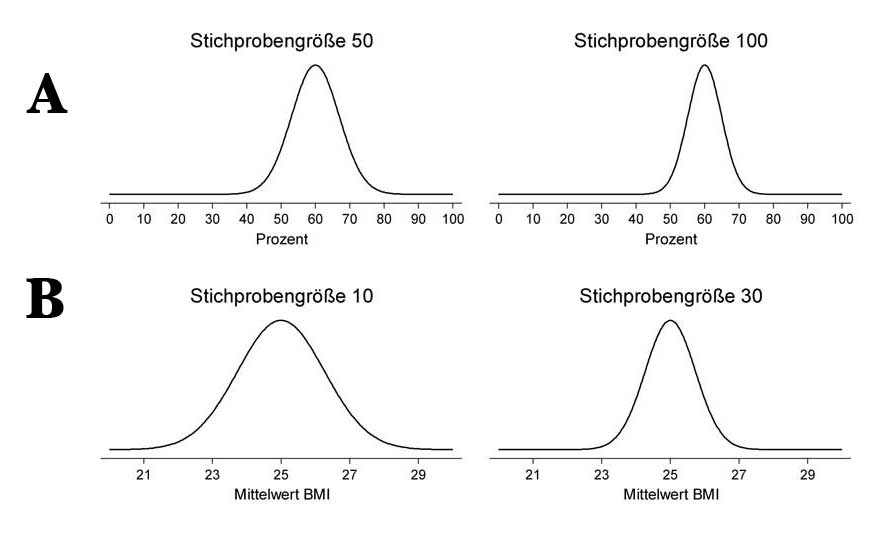
Web-Abb. 2.3.3 Normalverteilungskurven für die Stichprobenvariabilität in Abhängigkeit von der Stichprobengröße
a. Prozentsatz an verheirateten Personen; Stichprobengröße: 50 bzw. 100 Personen
b. BMI-Mittelwert; Stichprobengröße: 10 bzw. 30 Personen
Zusätzliche Formeln
Web-Formel 2.3.1 Formeln für die Berechnung des 95%-Vertrauensintervalls einer Proportion
Web-Formel 2.3.2 Formeln für die Berechnung des Standardfehlers und des 95% Vertrauensintervalls der Differenz zwischen zwei Mittelwerten sowie der Differenz zweier Proportionen
Web-Formel 2.3.3 Formeln für die Berechnung des 95% Vertrauensintervalls des relativen Risikos und der Odds Ratio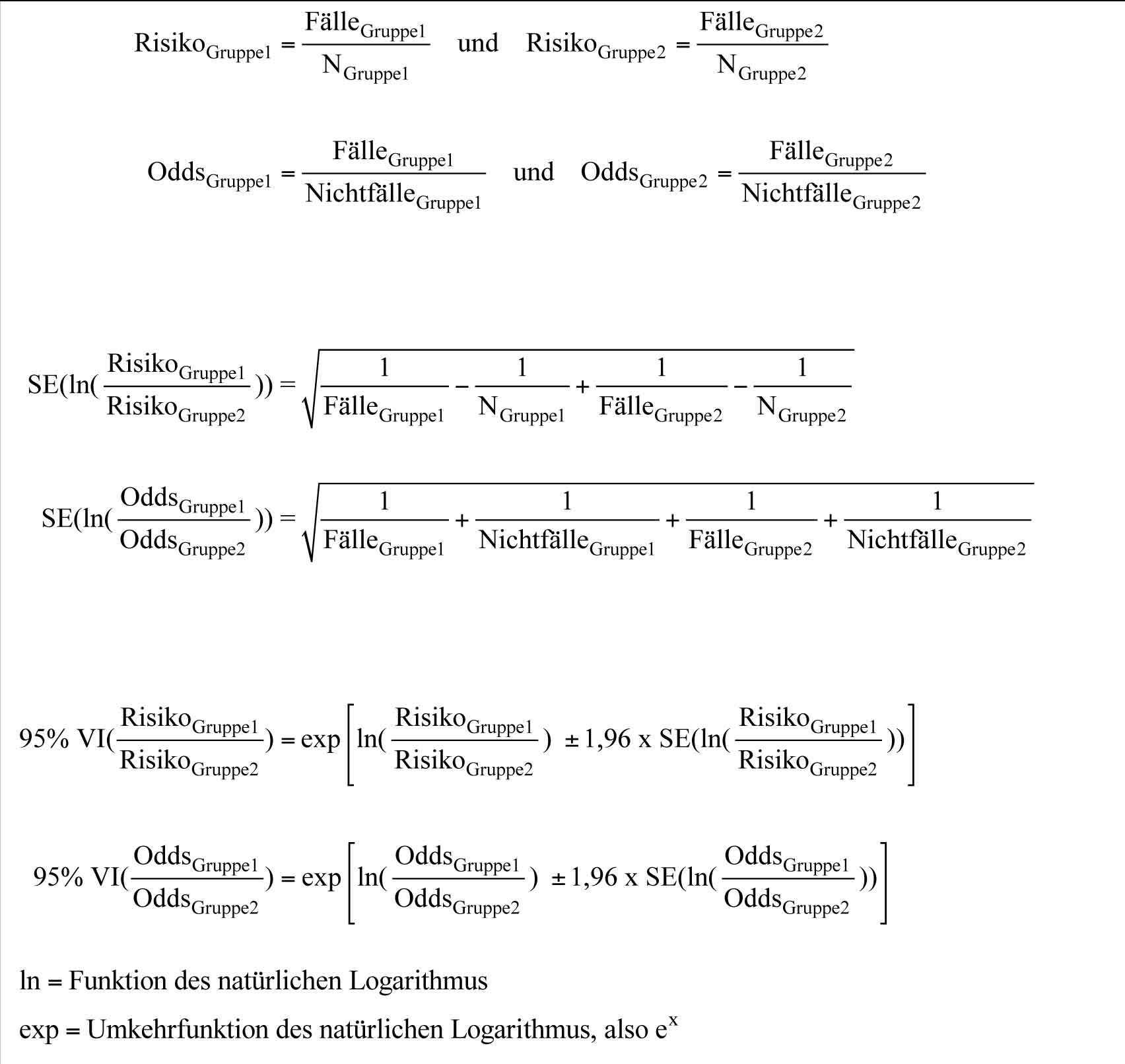
Web-Formel 2.3.4 Berechnung des p-Wertes für die Hypothese, dass die Differenz der wahren Mittelwerte zwischen zwei Gruppen exakt Null ist (MWGruppe1 – MWGruppe2 = 0) (s. a. Tab. 2.3.5)
Zusätzliche Tabellen
Web-Tab. 2.3.1 Flächenberechnungen mit Hilfe verschiedener Statistik-Software (R; Stata; Excel) für einen bestimmten Prozentsatz an Werten innerhalb der Normalverteilung bei vorgegebenem Mittelwert (MW) und vorgegebener Standardabweichung (SD)
Zusätzliche Boxen
(1) Ergänzende Box zu Kap. 2.3.7 Der Umgang mit Wahrscheinlichkeiten: Interpretation von Untersuchungen und Tests
Web-Box 2.3.1 Wichtige Rechenregeln für den Umgang mit Wahrscheinlichkeiten
P(A) steht für die Wahrscheinlichkeit (Probabilität), dass das Ereignis A eintritt oder zutrifft (= unbedingte Wahrscheinlichkeit).
P(A | B) steht für die Wahrscheinlichkeit von A, unter der Bedingung, dass B eintritt oder zutrifft (= bedingte Wahrscheinlichkeit).
- Nichtnegativität und Normierung: 0 ≤ P(A) ≤ 1
Wahrscheinlichkeiten sind nichtnegative, reelle Zahlen. Die Wahrscheinlichkeit eines sicheren Ereignisses ist 1, diejenige des unmöglichen Ereignisses ist 0.
- Komplementarität: P(A) = 1 – P(nicht A)
Die Wahrscheinlichkeiten zweier sich ausschließender Ereignisse sind komplementär, wenn entweder das eine oder das andere Ereignis eintreten muss (z.B. Tod oder Überleben zum Zeitpunkt des Studienendes; positives oder negatives Resultat einer Mammografie bei untersuchten Frauen).
- Multiplikation: P(A und B) = P(A | B) x P(B) = P(B | A) x P(A)
Die Wahrscheinlichkeit für das gemeinsame Eintreten der Ereignisse A und B lässt sich durch Multiplikation der bedingten Wahrscheinlichkeit des einen Ereignisses mit der (unbedingten) Wahrscheinlichkeit des anderen Ereignisses berechnen (Beispiele für solche Ereignisse wären Vorhofflimmern [A] und Schlaganfall [B] oder Brustkrebs [A] und positives Resultat einer Mammografie [B]).
- Addition: P(A oder B) = P(A) + P(B)
Die Wahrscheinlichkeit, dass entweder das Ereignis A oder das Ereignis B eintritt, ist gleich der Summe beider Einzelwahrscheinlichkeiten, wenn beide Ereignisse sich gegenseitig ausschließen (ein Beispiel hierfür wäre ein Sportler, der direkt nach einem Sportunfall entweder zu seinem Hausarzt [A] oder in die Notfallstation eines Krankenhauses [B] geht; beides ist gleichzeitig nicht möglich).
Internetquellen zum Thema
Freie Software zur Datenanalyse
(All accessed 17 October 2023)